NexusArcana

I think this is a not only an interesting topic but an easy one to grasps particularly because the mathematics is not hard, the harder the mathematics becomes is only because we are adding extra parameters and want to engage with Finner qualities of the circle. One of the reasons I choose this as a starting project because circle is so ubiquitous it has infinite value only because a circle is everywhere, when you want to investigate a deeper aspect of the technical/ mathematical aspect then it is possible only because we started with a nice easy functional foundation. So, with this article although is simples the template for how I hope to think and teach about things. I want to go for something called Mutiple reservation of the same thing because in essence a thing can have many different forms, yet its essence quality remains unchanged. one of the main meanings of abstraction is that in some instance it is the same thing but in a greater instance it stays part of it yet above it in the sense that it never touches a form. Shapes are a great way to discuss this because in the abstract we can conceive of a perfect circle yet in reality we have to contended with coverture and deformities.

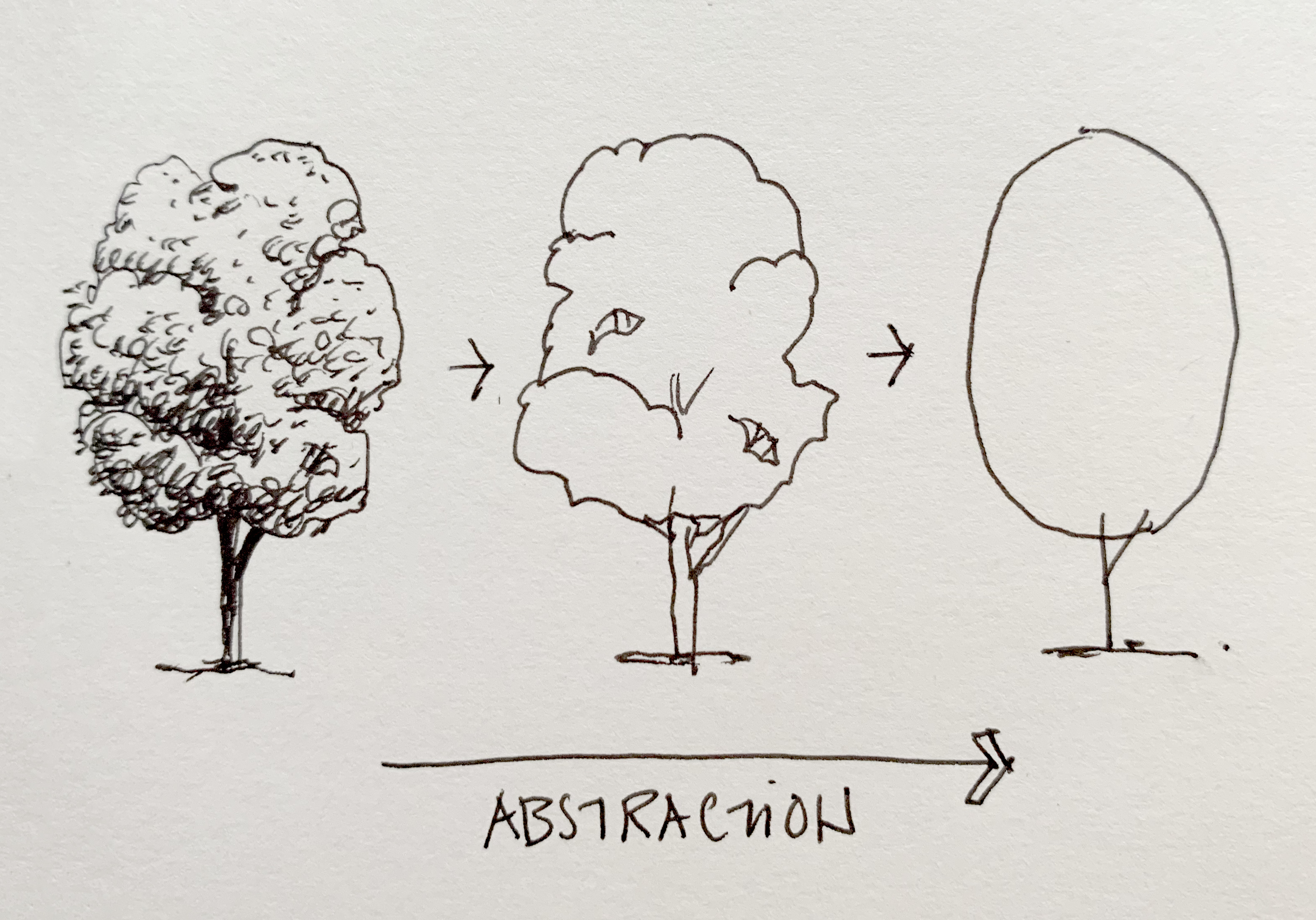
In my opinion I think mathematics creates the highest abstraction because it ensures a universe that is perfect and orderly in the fashion of creation and destruction of ideas mundane and divine. Mathematical physics, is next in terms of the concretion of ideas becoming things, next is the computational aspect of things which in term relies on the mathematical physics ground to make possible computational devices as representation of finite ideas, which may change to divine as quantum computation becomes a thing however that is beyond the scope of this problem; ideas of programs do things algometrical similarly we can conceive that DNA is a program that drives us algorithmically towards cause and end. Like grow human approaching some limit, typically between 18-25 if condition is met stop growing.

Because the circle has many properties, and the scope of this article is mathematical representation we will focus on that however some circles see this object as divine in nature and in the broad scheme of things because it encompasses all thing which are its in boundary yet comprise a singular unity as the number 1 which has many implications like is stated beyond the context of teaching in this format.

So, to reiterate my goal is to have teaching style that in multiple ways views the object of discussion by capturing instances of an abstract essence such that in all cases we can see the design withing the design so to speak.

MATHEMATICAL ‘

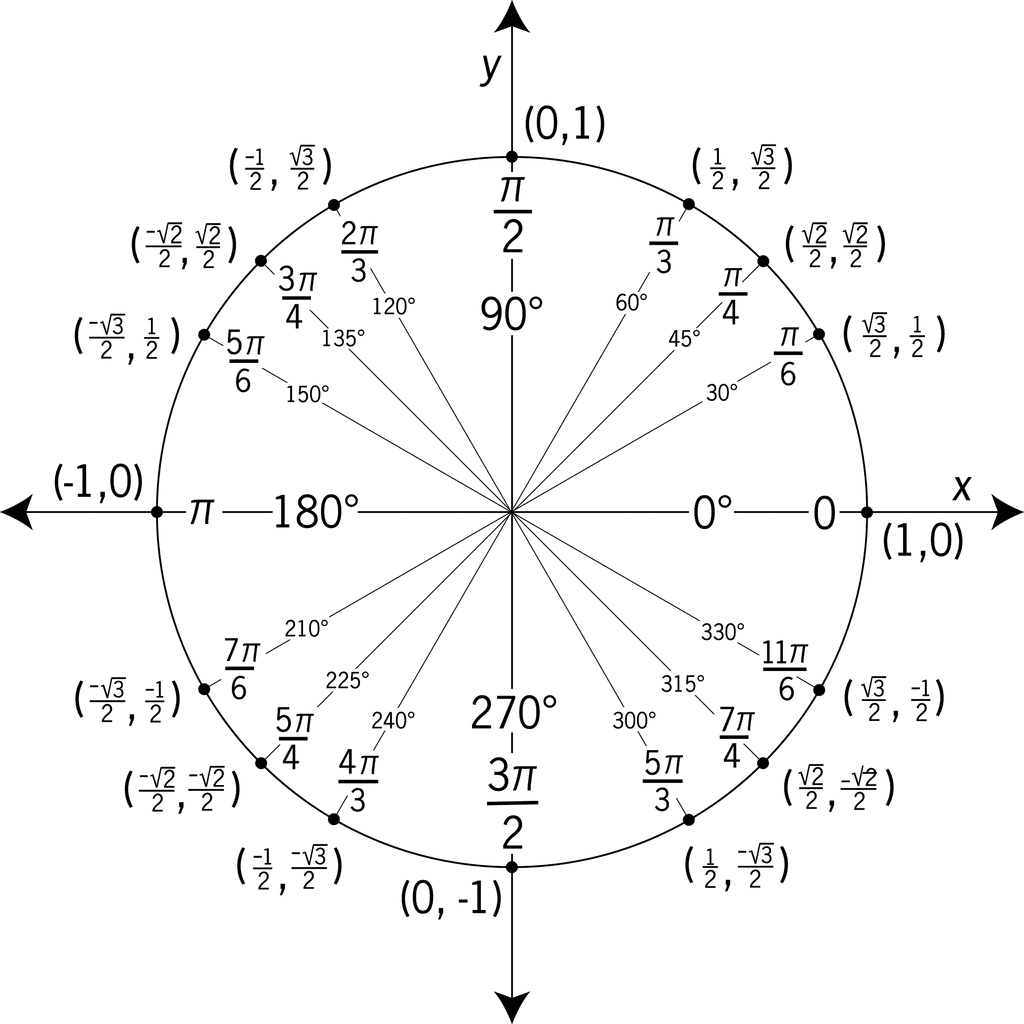
Definition :

A unit circle is a circle with a radius of 1, centered at the origin (0, 0) in the Cartesian coordinate system. It is used in mathematics, especially in trigonometry, to generalize trigonometric functions and find sine and cosine values given a point on the unit circle.

Definition : Semantics; the meaning or relationship of meanings of a sign or set of signs

This is important because its humans are time- binders, and we use signs and symbols across time and space to transmit information from the past to the present and to the present to the future. So, because I will be using many signs and symbols to illustrate points not just in this article but in many articles it important to understand why they are the way they are; I might write an article about that.

x^2 +y^2 =1

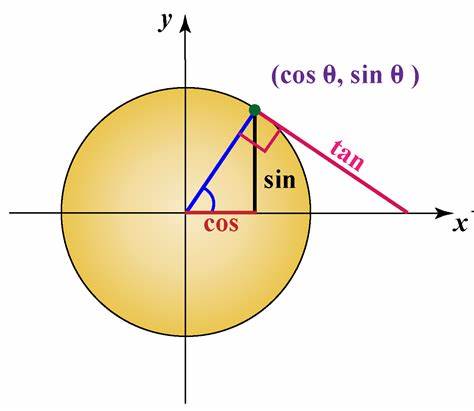
x can be thought of as a cosine, and y can be thought of as a y =1

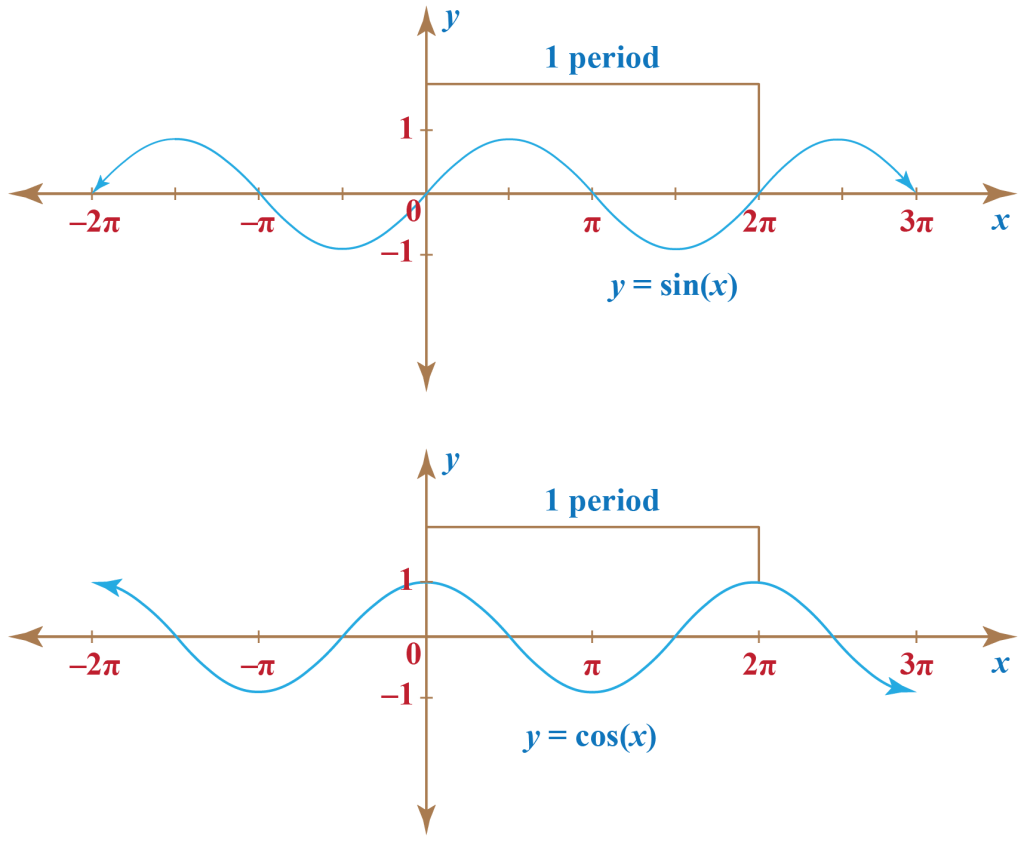
split the circle into values following the algebraic periodic motion and you get two graphs which correspond to the motion of a point moving along the circle we can label that point as P(X,Y) which is P(cos^2(x), sin^2(x))

by combining the algebraic splitting of the circle, we can represent it algorithmically as program

COMPUTATIONAL

def main():
    import numpy as np
    import matplotlib.pyplot as plt
    from matplotlib.widgets import Slider

    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=0.25)

    theta = np.linspace(0, 2*np.pi, 100)
    r = 1
    x = r * np.cos(theta)
    y = r * np.sin(theta)

    line, = ax.plot(x, y)  # Store the line object
    ax.set_aspect('equal')
    ax.set_xlim(-2,2)
    ax.set_ylim(-2,2)
    ax.axis('off')

    axradius = plt.axes([0.2,0.1,0.6,0.03])
    radius_slider = Slider(axradius, 'Radius ',0.1,2.0 , valinit=1)

    def update(val):
        r = radius_slider.val
        x = r * np.cos(theta)
        y  = r * np.sin(theta)


        line.set_xdata(x)
        line.set_ydata(y)
        fig.canvas.draw_idle()

    radius_slider.on_changed(update)  # Moved outside the update function

    plt.show()

if __name__ == "__main__":
    main()

Feel free to test the program take the code and run it into a PyCharm file or whatever software you have that can read a Py file. This article is a little messy but as I refine my presentation skills, I think you guys will in for some great treats.